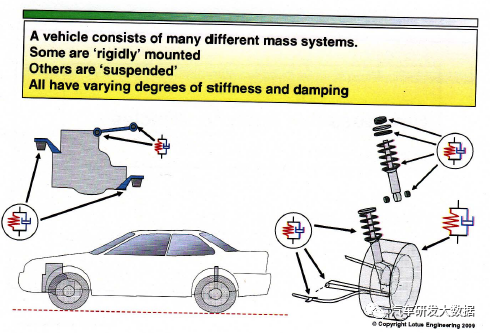
一、车辆垂向动力学模型
车辆和底盘之间的垂直力一般由以下几种情况造成,当车辆通过不平整的路面时,或车辆横向和纵向操纵时引起车体侧倾或俯仰,再或者由动力系统和轮胎/车轮运动的内部激励,其中最值得注意的是由于路面不平造成的垂向力。这些干扰力使车辆系统产生响应,可能不利于乘坐的舒适性。
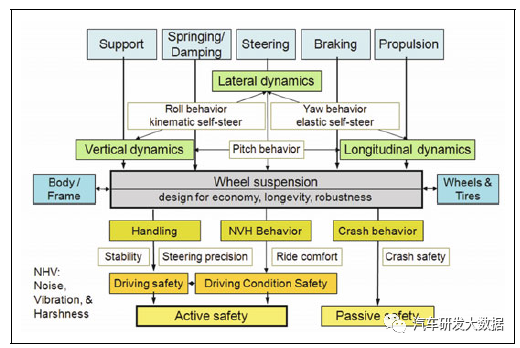
(图1 底盘系统和整车表现关系图)
如上图,底盘系统可分为垂向动力学模型、纵向力学模型和侧向动力学模型,模型之间存在侧倾、横摆和俯仰的相互作用,这些模型与操控、NVH、平顺性、碰撞、稳定性、转向精确等性能强相关。
有效规划垂直动态目标是减少车身加速度,减少侧倾和俯仰运动,减少垂直轮力变化,以及独立于车辆有效载荷的振动特性,汽车垂直动态目标的研究可以利用了适当的振动理论模型进行分析。关于底盘垂向动力学模型在很多书籍和培训中有着大量的说明,本文抛离理论公式的搭建,聊一聊动力学模型的应用。
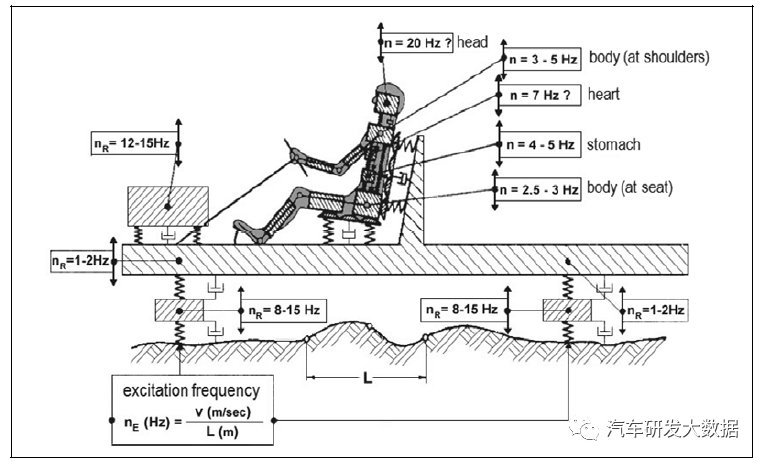
(图2 垂向动力学模型图例)
二、垂向动力学模型
2.1 相关零部件
垂向动力学模型相关零部件为弹簧、减震器、衬套、topmpunt和缓冲块等部件,其中不同的悬架形式与布置形式会存在一些差异。
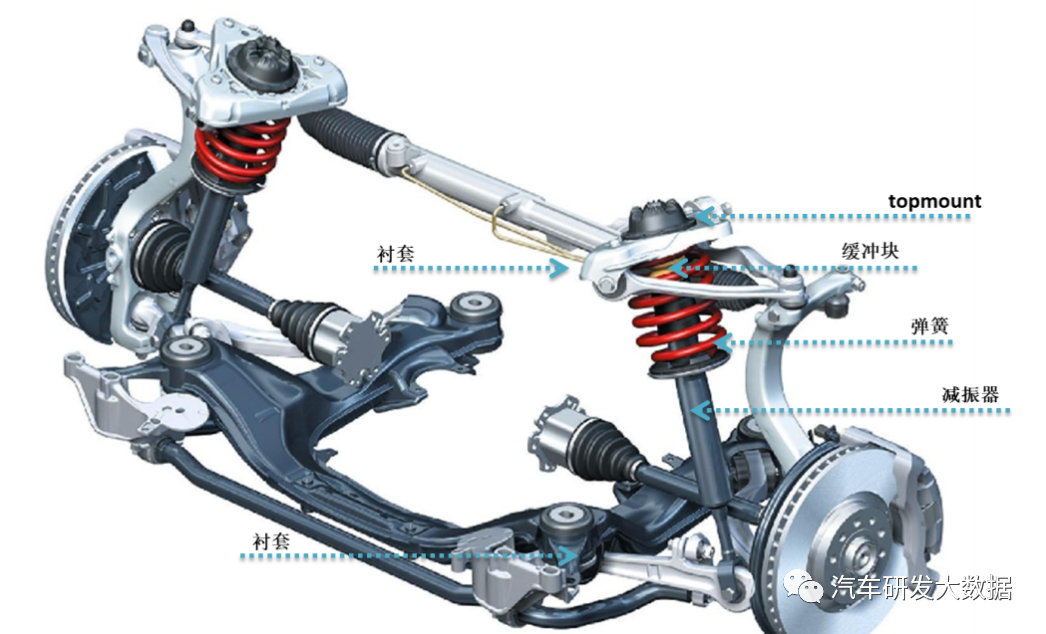
(图3 垂向动力学模型相关组件)
垂向动力学模型主要刚度(弹簧)与阻尼(减震器)构成,并且考虑布置关系,弹簧和减震器是否分开安装,或布置在那个臂上,弹簧和减震器前后左右的位置关系,不同的布置形式主要影响杠杆比和受力方向。其中赛车和超级跑车的弹簧横向布置是非常特殊的,其目的也是降低车身Z向高度,通过机构将力传递至Z向。
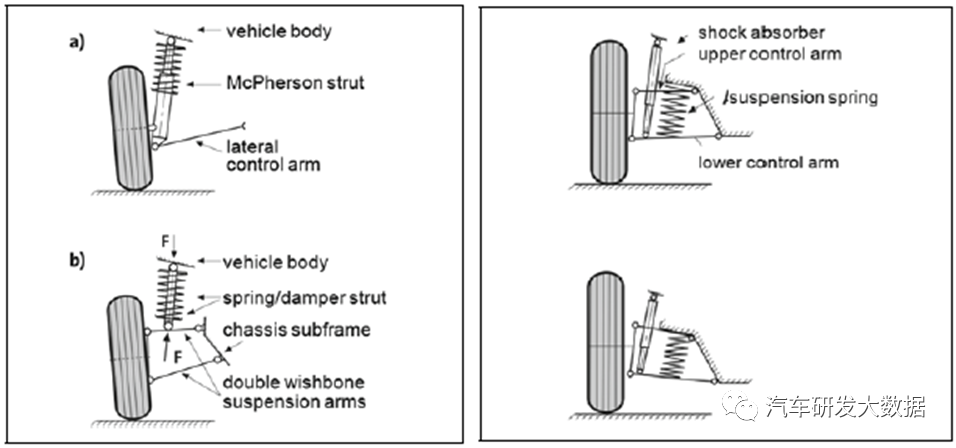
(图4 弹簧与减震器布置图例)
2.2 动力学模型要素
弹簧刚度:本质是支撑本身,同时是垂直方向最核心的舒适性部件,乘用车的偏频是参考人走路频率设计1HZ这个基准,就是取决以弹簧的设计。弹簧的刚度是线性的,汽车上很少有非线性的弹簧,所以我们在悬架系统设计上更关心弹簧力学轴线、弹簧杠杆比、前后悬架的偏频(双自由度模型)以及匹配(三自由度模型)的俯仰问题。
本质是支撑车身,就是取决以弹簧的设计。弹簧的刚度是线性的,汽车上很少有非线性的弹簧,所以我们在悬架系统设计上更关心弹簧力学轴线、弹簧杠杆比、前后悬架的偏频(双自由度模型)以及匹配(三自由度模型)的俯仰问题。
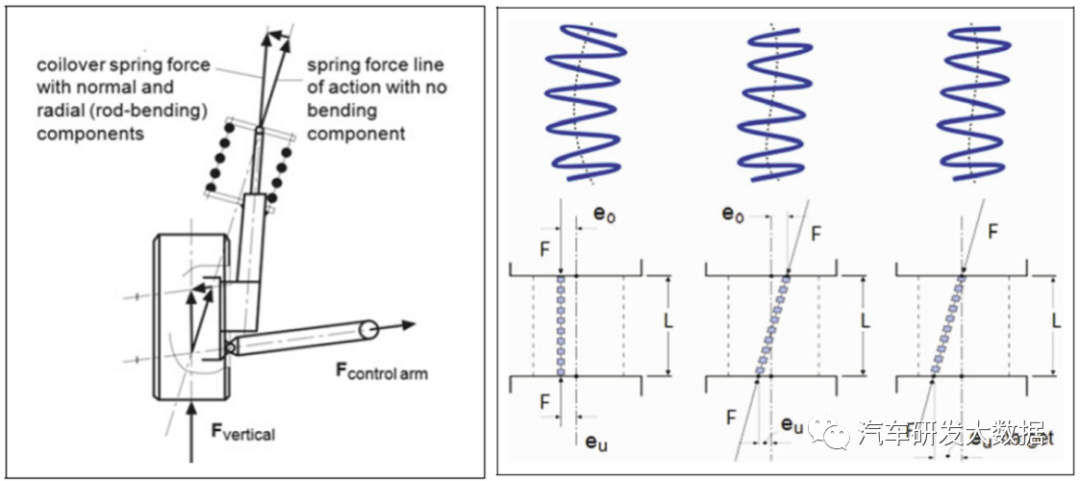
(图5 弹簧力学轴线)
衬套刚度:衬套作为隔振的单元,既要满足悬架几何结构中力的传递,同时兼顾悬架的C特性,所以在底盘衬套设计静刚度过程中均需要考虑。下图描述的是不同结构衬套刚度的变化情况,可以简单的总结一下,如下表。
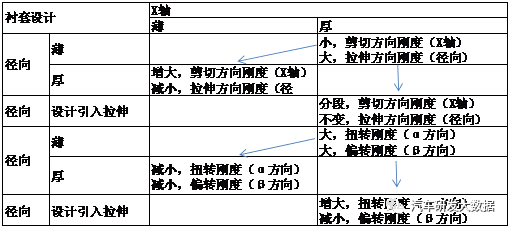
(表1衬套刚度和结构的关系)
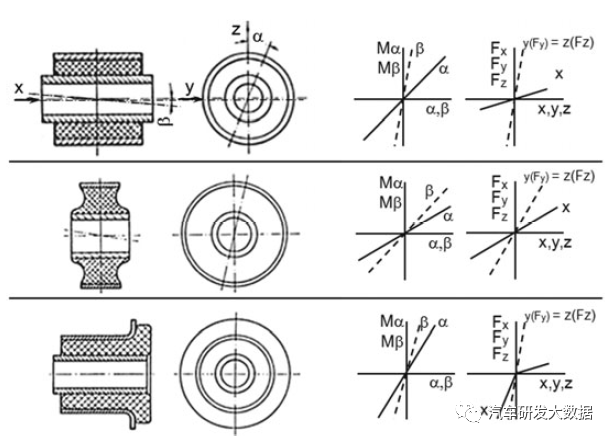
(图6 衬套刚度和结构的关系)
减震器阻尼:对因路面不平或驾驶提哦爱爱你差而引起向车身传递的振动进行收敛,快速消除由路面引起的轴和车轮的振动,保证车轮随时抓住地面,保证车辆有效的转向和刹车功能。
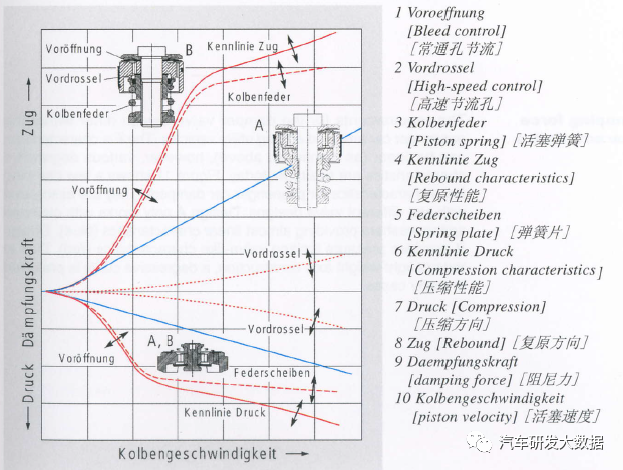
(图7 减震器阻尼和结构的关系)
缓冲块刚度(Rebound and Compression Bump Stops)
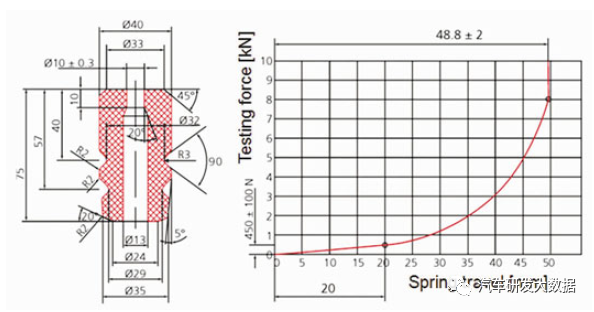
(图8 缓冲块刚度特性)
迟滞:
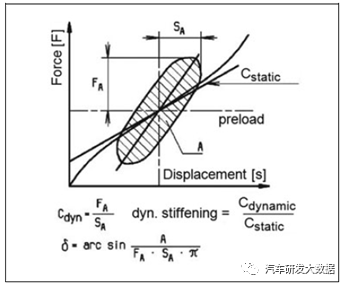
(图9 迟滞特性)
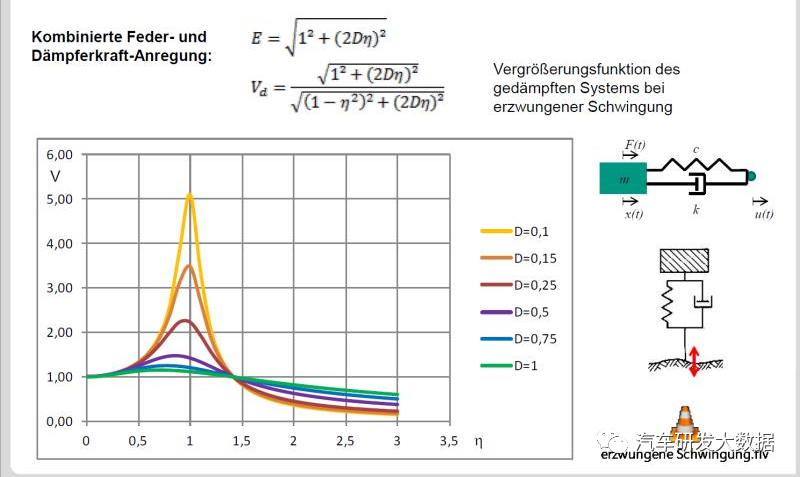
2.3 垂向动力学模型
垂向动力学模型有很多种,需要解决问题的场景来判定模型是否符合。
(图10 动力学模型简图)
准静态模型:为了分析悬架系统的零部件设计是否合理,同时确定悬架模型的准确性,先要建立静态模型,这个模型的特点在于簧上质量是被固定的,所以并不能体现簧上质量的振动情况,但可以体现传递过来的力的变化情况。
单自由度模型:不考虑簧下质量的自由度,路面输入通过悬架系统之间传递到簧上质量,研究簧上质量的Z向振动情况。
(图11 单自由度模型简图)
双自由度模型:考虑簧下质量的自由度,路面输入通过轮胎传递至悬架,悬架系统之间传递到簧上质量,研究簧上质量的Z向振动情况。同时在幅频出现簧下质量振动峰值。
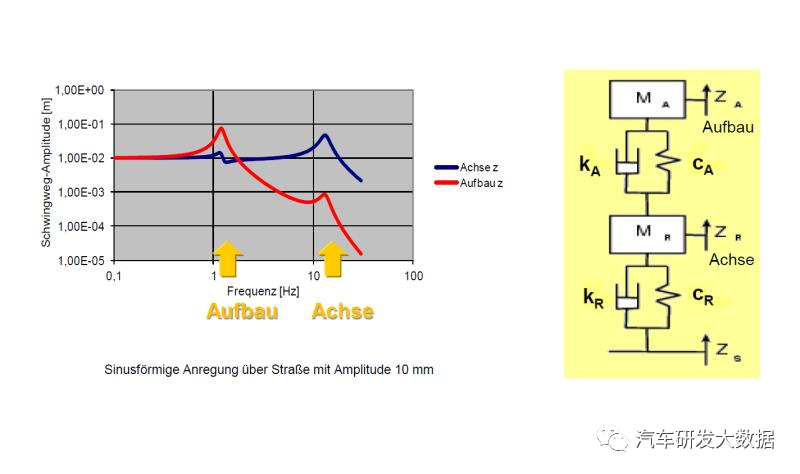
(图12 双自由度模型简图)
多自由度模型:为了研究整车的舒适性,垂向动力学模型有研究Z向振动、俯仰、侧倾和单轮跳等,根据不同的工况设置多种自由度模型。
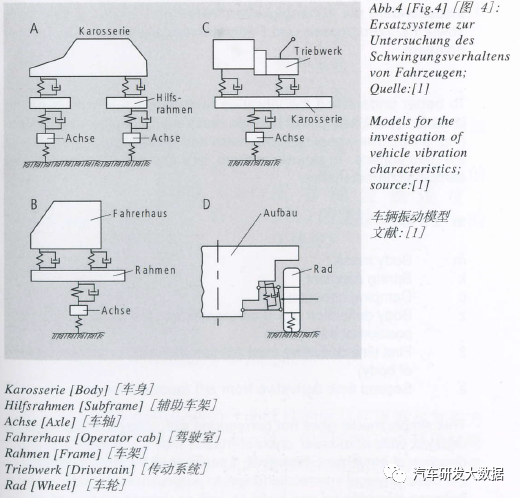
(图13 多自由度模型简图)
三、实际开发的应用
3.1 基本模型应用
底盘振动模型有两类基础模型:kelvin模型和gehmann模型。
kelvin模型:用户描述弹簧和减震器力学关系模型,单通道悬架就属于此类型模型。
gehmann模型:用于近似描述橡胶衬套的模型,双通道悬架就属于此类模型。
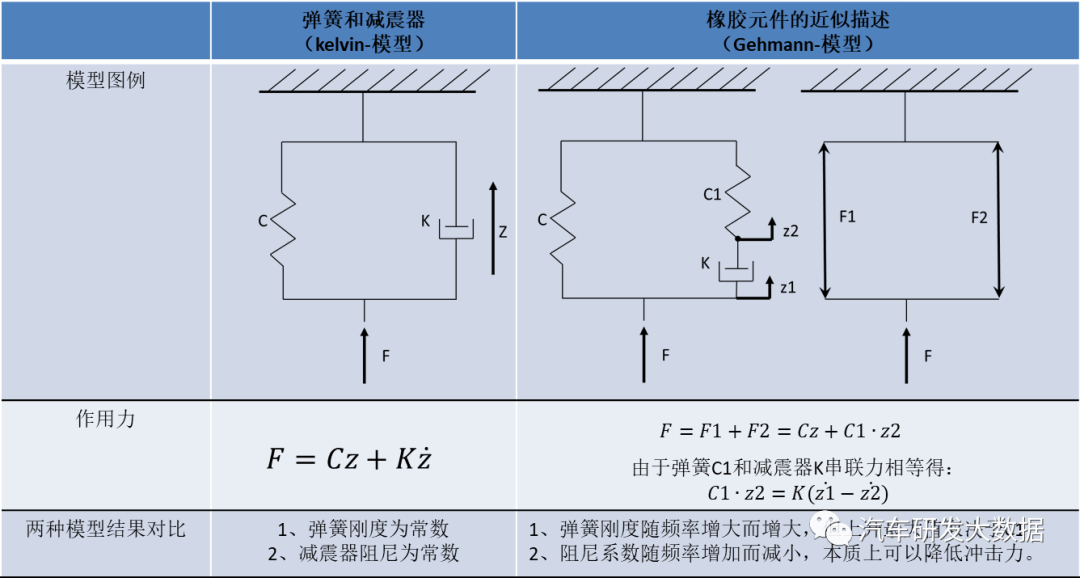
(表2 基础模型简图)
弹簧与衬套刚度模型符合串联与并联关系。
串联型:K = (K1·K2)/(K1 + K2)
并联型:K = K1 + K2
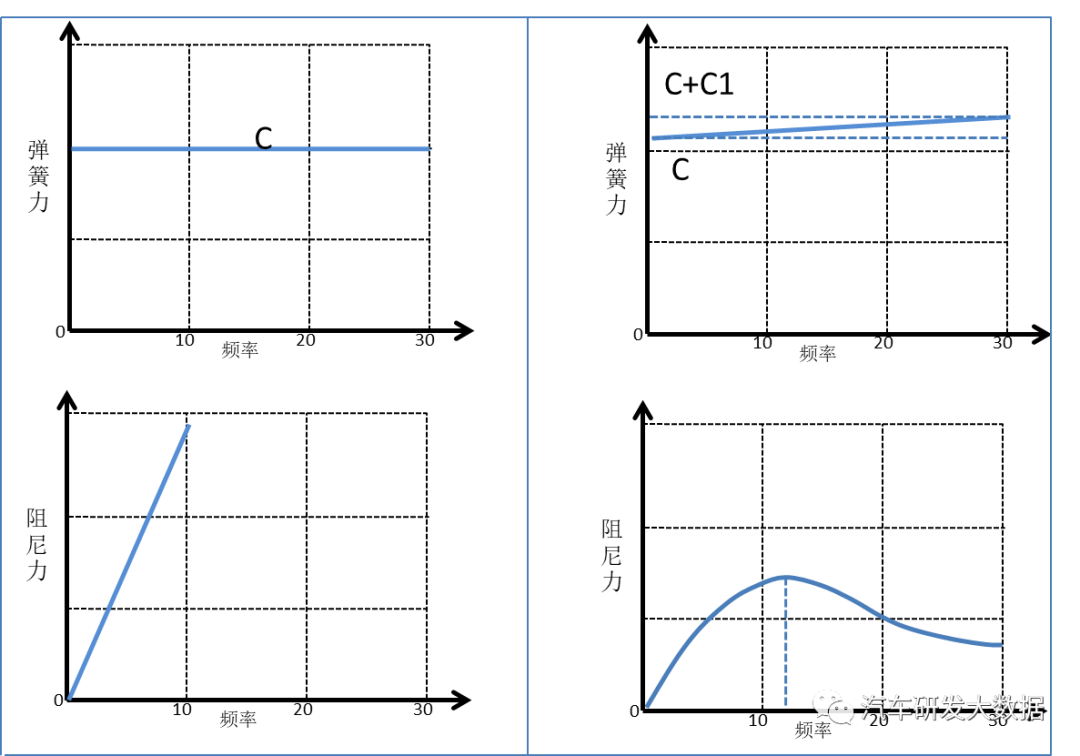
单通道设计原理:减震器和弹簧作用在同一点,弹簧和减震器位移量相同,符合kelvin模型,单通道悬架已经慢慢被双通道设计替代,核心就在于随着频率的增加阻尼不会变化,造成冲击感明显,但又很难通过减震器优化。
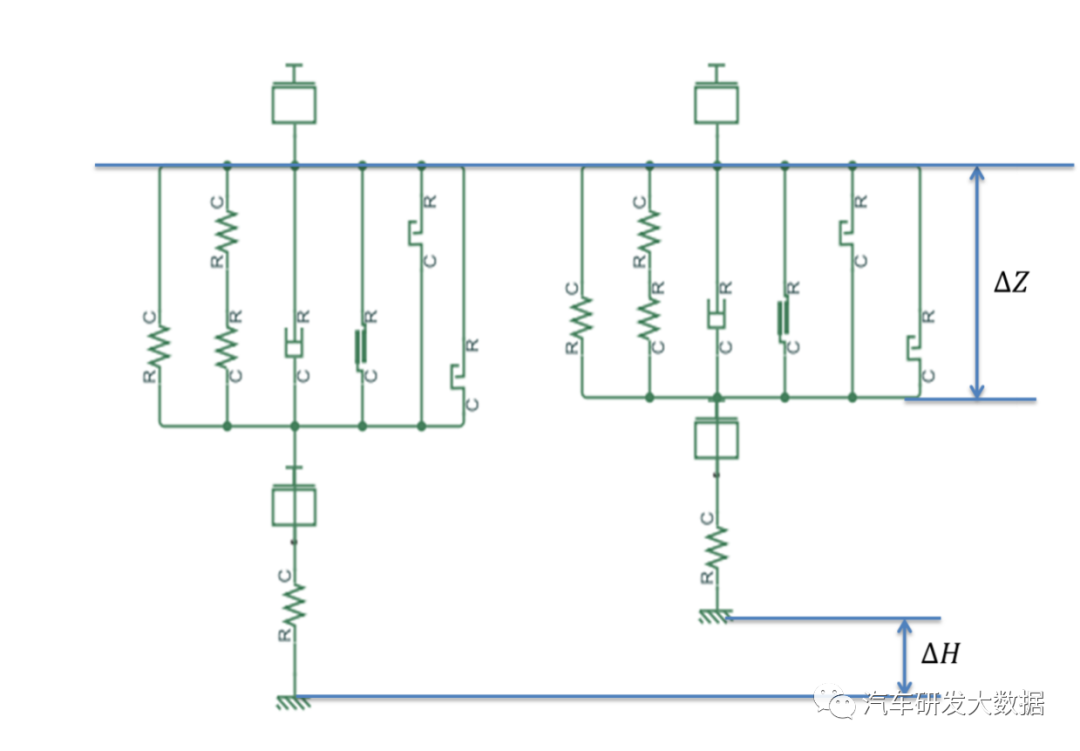
(图14 单通道悬架模型)
双通道设计原理:减震器和减震器作用分别从两条路径传递到车身,同时,弹簧和减震器变形长度并不相同,符合gehmann模型,当频率不断增大,阻尼力会先增大后减小的趋势,有效的克服路面高频率小幅值带来的振动,可以大大提高舒适性,所以对于双通道topmount刚度设计就需要此类模型,建议双通道悬架可以带着topmount做阻尼力测试。
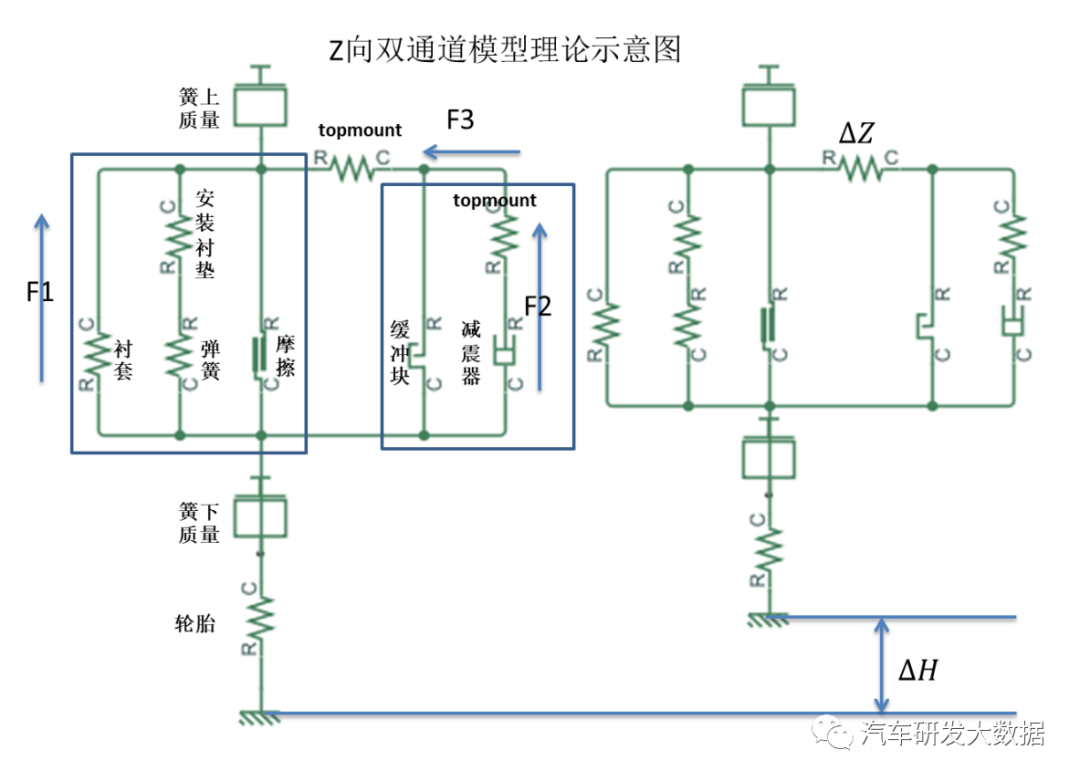
(图15 双通道悬架模型)
衬套动刚度设计原理:大多数衬套刚度是gehmann模型,静刚度C,动刚度极值是C+C1,还有很多复杂的衬套模型,这里就不过多阐述。
3.2 准静态模型应用
底盘系统的KC测试是作为底盘的STS性能管控各个底盘系统行为最为核心且基础的指标,有效的解读KC曲线可以清晰的解释系统及设计的各项指标,同时可以搭建相关的数学模型或仿真对标,达到性能分解的目的,KC台驾可以理解是准静态的垂向动力学模型。
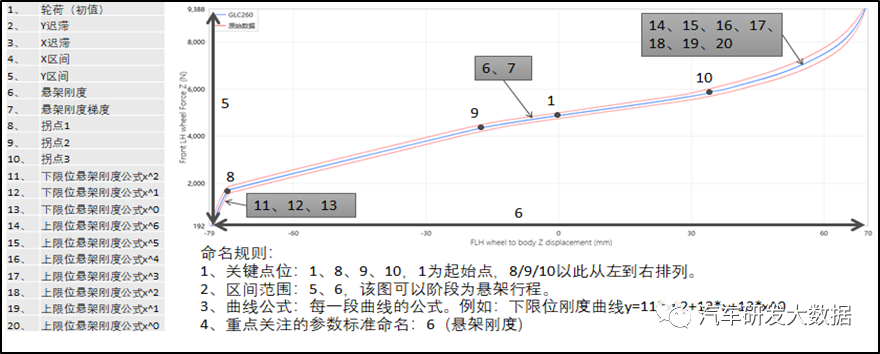
(图16 悬架刚度K特性)
准静态模型是建立振动分析的基础上,必须建立符合工程设计的模型才能够更准确的分析悬架系统的特性,由于前期对标过程中仅有KC特性参数,所以建立准静态模型就尤为重要。
根据悬架设计的基础,建立弹簧、衬套、减震器、摩擦等数字模型,本例通过matlab建立悬架模型,通过对标KC曲线,达到STS分解到CTS的目的。下图为悬架准静态模型,建模思路如下。
- 路面或台驾Z向输入采用sin函数,频率0.02HZ,足够低才能更接近静态状态,并且加一个时间滞后,数学系统需要稳定时间。
- 输入求导,计算速度作为减震器阻尼的输入。
- 输入求导作为摩擦判定依据,定义初始迟滞。
- 建立双通道缓冲块的力需要传递到topmount上,造成topmount位移致使缓冲块的接触位置变化,是一个动态的过程,所以需要建立一个循环过程。
- 上下缓冲块需要建立触碰的间隙要求,通过逻辑判断公式达到按接触间隙确定上下缓冲块起作用时间。
- 对于准静态模型预载没有实际的作用,更像是在做坐标平移,但此模型用于动态分析时,预载就有实际作用,同时模型需要以下增加重力和簧上质量位移的计算闭环。
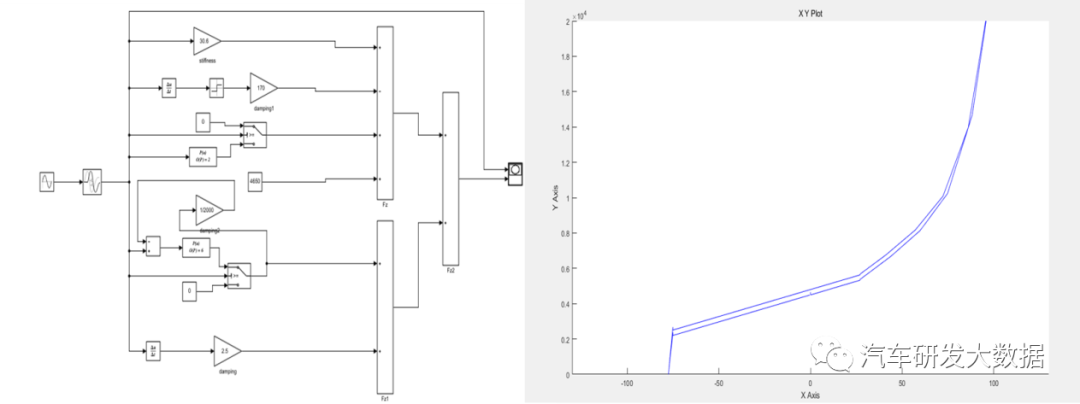
(图17 双通道悬架实际模型与结果)
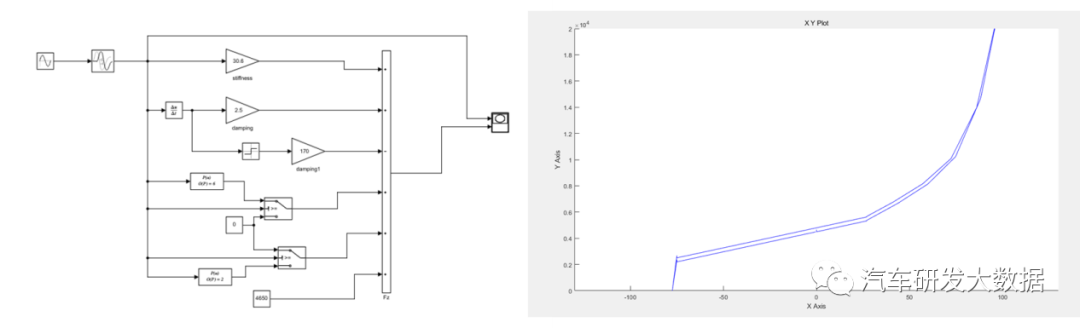
(图18 单通道悬架实际模型与结果)
3.3 双自由度模型
底盘系统双自由度模型:我们可以理解为就是现在我们常用的簧上簧下的频率计算公式,为什么要用数学模型呢,因为简化算法的判定依据来源于数据库的对标统计,这种计算方式不能满足高端悬架设计、电控功能校核以及控制逻辑的搭建。
(图19 双自由度模型应用场景)
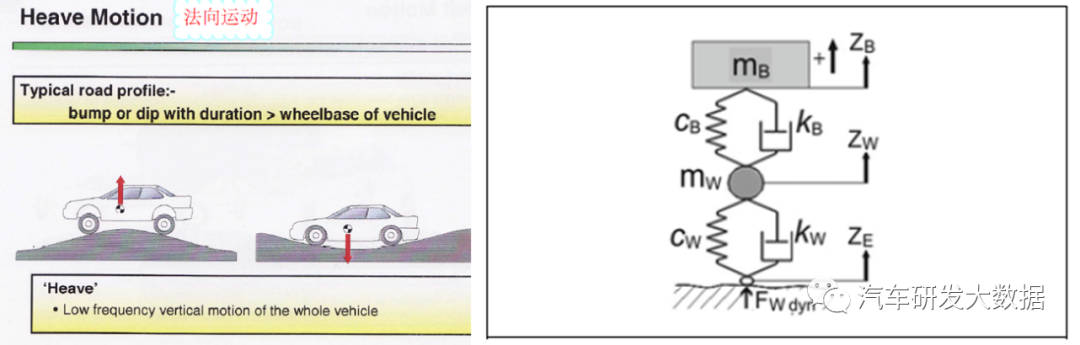
3.4 俯仰模型
高速公路的输入是连续的长波,波长从1m到100m都有,由于在高速公路上高速行驶,前后轮胎在经过同一个波存在着一定滞后时间,而这个滞后不能让车辆俯仰同时需要快递的收敛,这就需要俯仰模型的校核,此模型涉及到前后悬架的偏频匹配,大多数公司使用简化的俯仰模型匹配长波路面,简化版的模型只有力的平衡,并不包含速度和角速度,所以没有办法引入转动惯量,造成很多车型计算匹配和实际调教存在偏差。
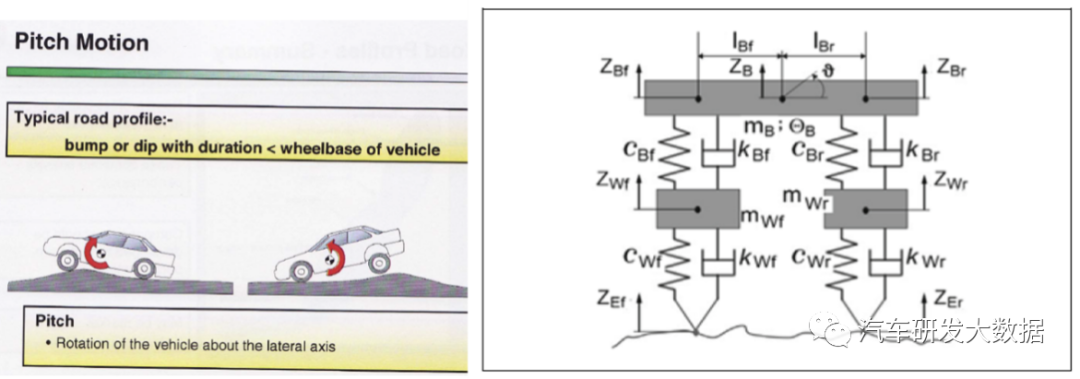
(图20 俯仰模型应用场景)
3.5 侧倾模型
侧倾模型主要是研究车辆侧倾匹配是否合理,当前后悬架的刚度设定后需要设计侧倾提督变化(例如4deg/g),简单的侧倾模型可以评估侧倾所需要的总刚度,但当我们考虑到侧倾和横摆的匹配关系时,就需要考虑质心高、前后侧倾刚度及侧倾刚度比,也可以考虑车体的扭转刚度,这也是我们底盘对车身扭转刚度提出的需求,如下图:
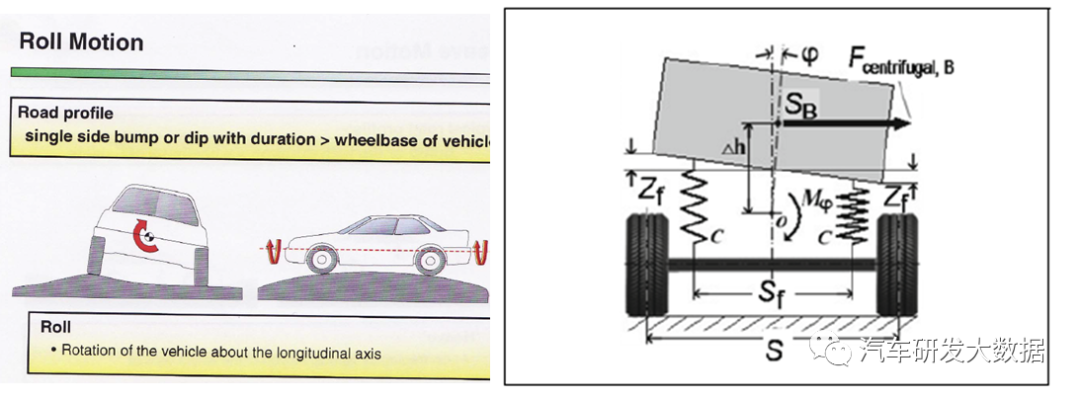
(图21 侧倾模型应用场景)
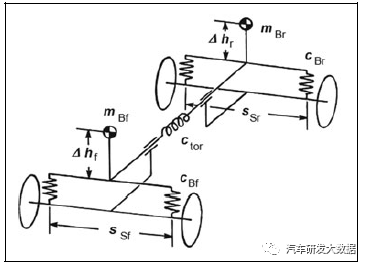
(图22 复杂侧倾模型)
3.6 单轮跳动模型
为什么考虑单轮跳,在主观评价中有种现象headtoss,评价驾驶员头部的侧向力,这个评价就是依据单轮跳动工况。
由于悬架在平跳和侧倾工况下,稳定杆存在参与和不参的区别,所以平跳舒适性和侧倾控制是存在矛盾的,平跳需要刚度低,而侧倾需要控制住车身侧倾角,所以稳定杆参与控制后得悬架刚度是平跳时的悬架刚度的两倍,这样就会造成一边轮胎过坑过坎时,稳定杆刚度大的悬架,headtoss现象严重,而稳定杆刚度低,侧倾控制又会变差,如果用调大弹簧降低稳定杆刚度又会造成平跳工况不舒适,所以我们需要研究单边轮胎模型寻求折中方案,值得一提的是电机驱动的主动稳定杆核心就是解决这个问题。
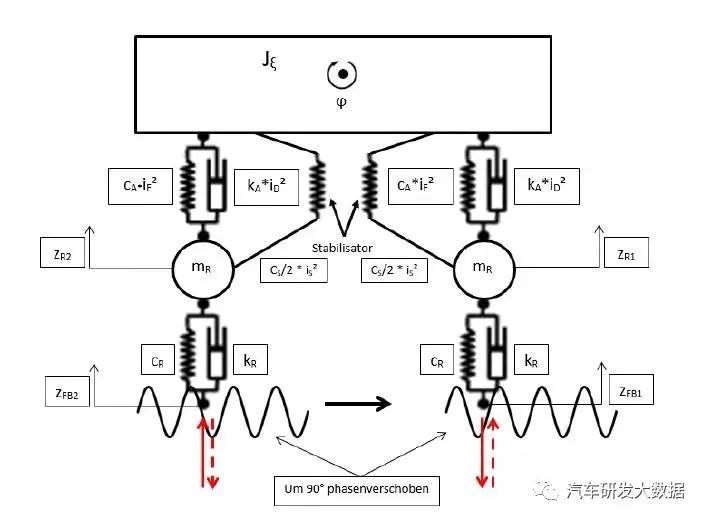
(图23 单轮跳模型)
3.7 冲击模型
冲击模型需要考虑纵向受力的几何、悬架刚度以及减震器布置角度,重点研究过坎时的舒适性。
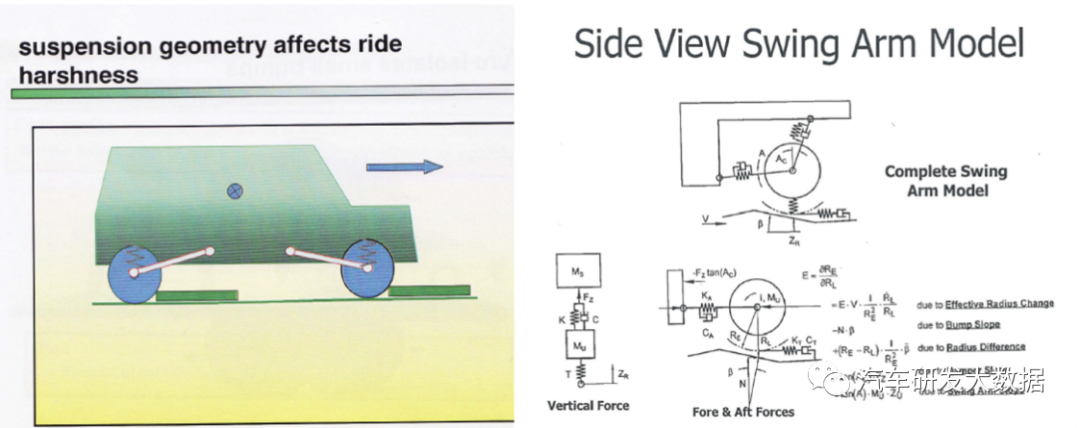
(图24 冲击模型应用场景与模型)
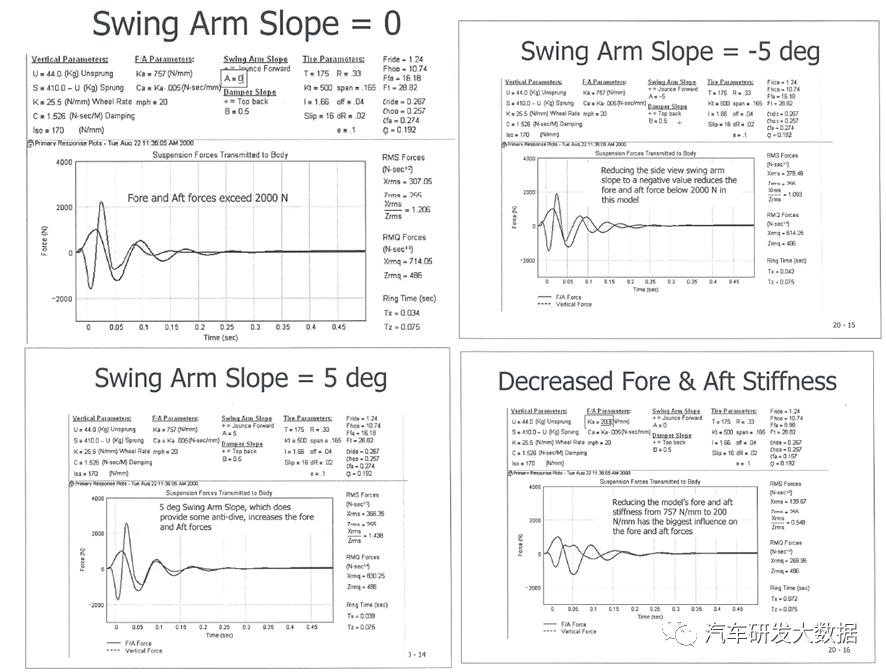
(图25 冲击模型应用与对比)
总之车辆开发需要这些模型,从逆向设计到对标设计,我们需要向正向去转变,各个主机厂已经有了大量的对标数据,再通过模型的校验,我们可以更加清晰的理解汽车垂向设计的边界和红线,也许超越并不是难事。

